mtuition

Understanding Torsional Shaft Dynamics

The purpose of any dynamometer is to apply torque and speed patterns to the unit under test (UUT). So, the quantity of fundamental interest is the torque delivered at UUT side. This is not the same as the torque being produced by the load motor. Mechanics in between load and UUT play an important role in defining dyno behavior. It should be the first thing any test bench designer considers. Unfortunately, all too often, it is considered and afterthought, especially as it comes to torsional virbrations.

Radial and torsional vibrations

There are two important vibration modes when considering a shaft design. Radial vibrations concern shaft off-center displacements. Torsional vibrations concern torque transmission from load to UUT.

Shaft Torsional Behavior

A simple first-order model considers an ideal coupling between load and UUT that is infinitely stiff. Relations between the angles \theta_L and \theta_U, respectively the angle of load and UUT with respect to their position at rest, and the external torques T_L and T_U, respectively exerted on load and UUT, are given by

\frac{\text{d}^2\theta_L}{\text{d}t^2}=\frac{\text{d}^2\theta_U}{\text{d}t^2}=\frac{T_L+T_U}{J_L+J_U} (1)

Load and UUT are therefore always perfectly in lockstep.

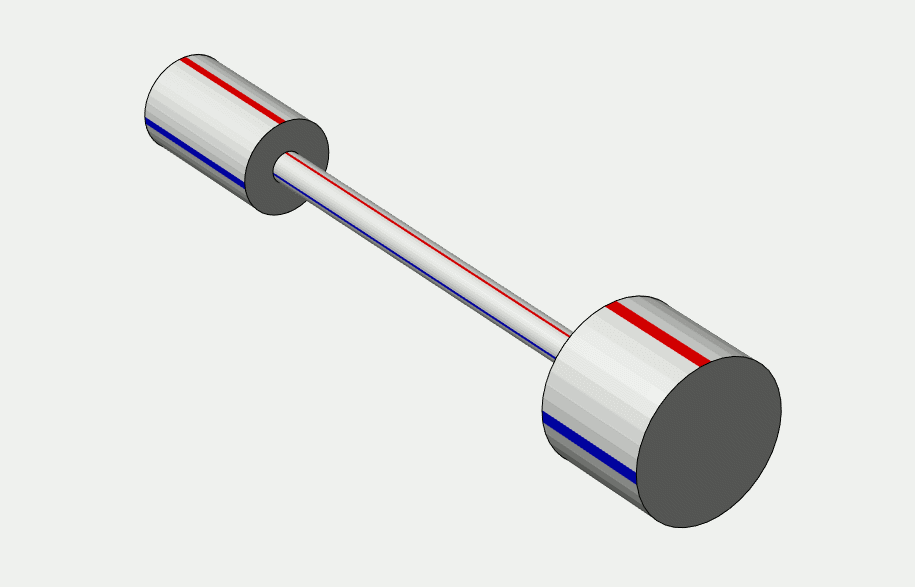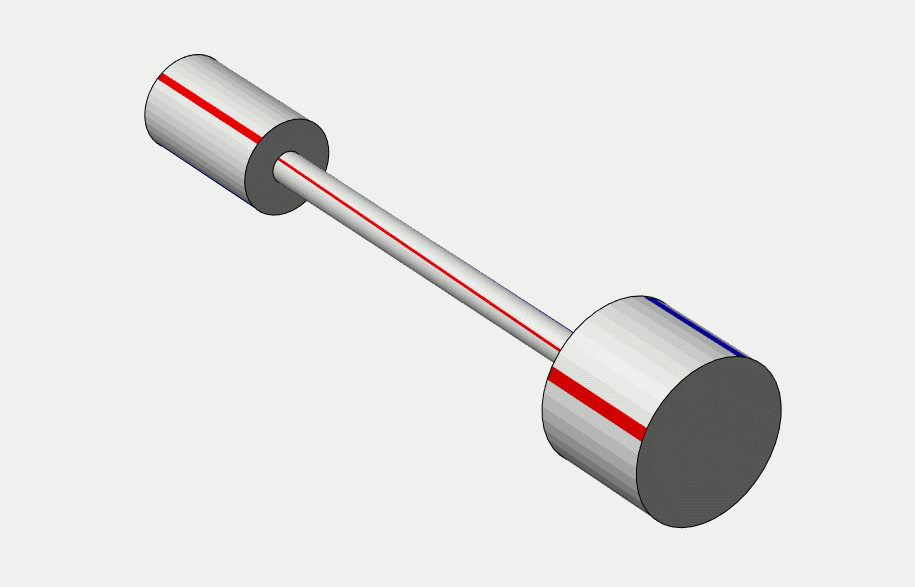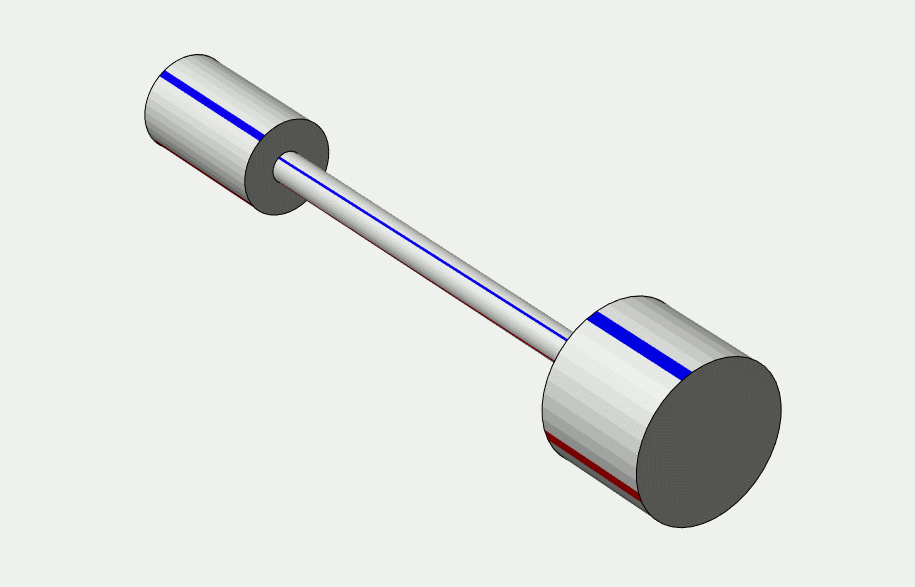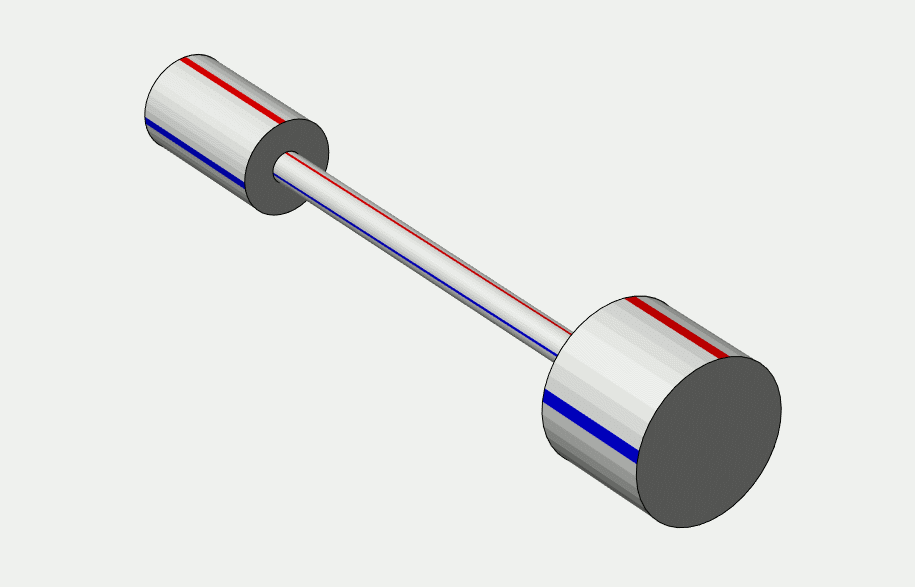
Mechanical couplings and shafts, however, are never ideal and therefor not infinitely stiff. In reality, the UUT-coupling-load assembly behaves as a mass-spring-mass system. As shown in the figure below, the shaft that couples load and UUT needs a difference in the angle displacements at both ends in order to transfer torque. It behaves as a torsion spring. Without a difference in angle across the coupling, there can be no torque.

Mathematically, this is described as

J_{L}\frac{\text{d}^{2}\theta_{L}}{\text{d}t^{2}} = T_{L}+ \kappa\left(\theta_{U}-\theta_{L}\right) (2)
J_{U}\frac{\text{d}^{2}\theta_{U}}{\text{d}t^{2}} = T_{U}-\kappa\left(\theta_{U}-\theta_{L}\right) (3)

The behavior of this system can be decomposed into a common-mode component and a differential mode component. The common mode component captures the displacement that UUT and load have in common. The differential mode component captures how the coupling is torted in order to transfer torque between UUT and load. Mathematically, they are defined by

\bar{\theta}=\frac{J_{L}}{J_{U}+J_{L}}\theta_{L}+\frac{J_{U}}{J_{U}+J_{L}}\theta_{U} (4)

and

\Delta\theta=\theta_{U}-\theta_{L} (5)

The common-mode angle is weighted with respect to the inertias. This simplifies its dynamic behavior which is captured by

\left(J_{L}+J_{U}\right)\frac{\text{d}^{2}\bar{\theta}}{\text{d}t^{2}} = T_{L}+T_{U} . (6)

This reflects the simple first-order behavior of a system with an infinitely stiff coupling. The angle difference across the coupling is governed by

\left(\frac{1}{J_{L}}+\frac{1}{J_{U}}\right)^{-1}\frac{\text{d}^{2}\Delta\theta}{\text{d}t^{2}} = -\kappa\cdot\Delta\theta + \frac{J_{U}\cdot T_{L}+J_{L}\cdot T_{U}}{J_{L}+J_{U}}. (7)

This equation corresponds to that of a harmonic oscillator excited by the torque inputs T_L and T_U. A non-stiff coupling therefore introduces a torsional vibration. The impact of this vibration on load and UUT behavior follows from

\theta_{L} = \bar{\theta} - \frac{J_U}{J_L + J_U}\Delta\theta (8)
\theta_{U} = \bar{\theta} + \frac{J_L}{J_L + J_U}\Delta\theta (9)

These equations show an important lesson: the side with the biggest inertia has least impact on differential torsion but is also least impacted by it. For example, if J_U \ll J_L, it follows from (7) that T_U has the biggest impact on the vibrational component \Delta\theta while (9) shows this component to heavily couple into the behavior of \theta_U. On the other hand, $lates T_L$ has a reduced impact while \theta_L is ony marginally impacted. As we will see next, this has important consequences for the design of both load and coupling.

Shaft Torsional Design

Because of their destructive capabilities, a lot of attention is given to the impact that shaft and coupling designs have on radial vibrations. However, the torsional design is often overlooked and is only considered when problems occur, often at startup of the bench. By that time, however, it may be too late as there is only so much you can do once the mechanical design of the coupling and the electromagnetic design of the load motor are fixed.

Piet
,